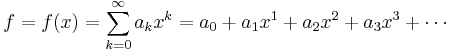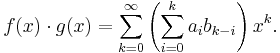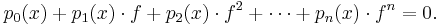Chomsky–Schützenberger theorem
In formal language theory, the Chomsky–Schützenberger theorem is a statement about the number of words of a given length generated by an unambiguous context-free grammar. The theorem provides an unexpected link between the theory of formal languages and abstract algebra. It is named after Noam Chomsky and Marcel-Paul Schützenberger.
Statement of the theorem
In order to state the theorem, we need a few notions from algebra and formal language theory.
A power series over  is an infinite series of the form
is an infinite series of the form
with coefficients 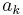 in
in 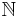 . The multiplication of two formal power series
. The multiplication of two formal power series  and
and  is defined in the expected way as the convolution of the sequences
is defined in the expected way as the convolution of the sequences 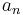 and
and 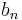 :
:
In particular, we write 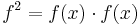 ,
, 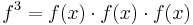 , and so on. In analogy to algebraic numbers, a power series
, and so on. In analogy to algebraic numbers, a power series  is called algebraic over
is called algebraic over 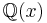 , if there exists a finite set of polynomials
, if there exists a finite set of polynomials 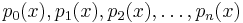 each with rational coefficients such that
each with rational coefficients such that
Having established the necessary notions, the theorem is stated as follows.
- Chomsky–Schützenberger theorem. If
 is a context-free language admitting an unambiguous context-free grammar, and
is a context-free language admitting an unambiguous context-free grammar, and 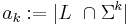 is the number of words of length
is the number of words of length  in
in  , then
, then 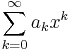 is a power series over
is a power series over 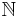 that is algebraic over
that is algebraic over 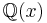 .
.
Proofs of this theorem are given by Kuich & Salomaa (1985), and by Panholzer (2005).
References
- Chomsky, Noam & Schützenberger, Marcel-Paul: "The Algebraic Theory of Context-Free Languages," in Computer Programming and Formal Systems, P. Braffort and D. Hirschberg (eds.), North Holland, pp. 118–161, 1963. Available online.
- Kuich, Werner & Salomaa, Arto: Semirings, Automata, Languages. Springer, 1985.
- Panholzer, Alois: "Gröbner Bases and the Defining Polynomial of a Context-free Grammar Generating Function." Journal of Automata, Languages and Combinatorics 10:79–97, 2005.